Objective
To develop a model that predicts the risk of 30-day, all-cause readmission in Medicaid patients hospitalized for heart failure.
Design
Retrospective study of a population cohort to create a predictive model.
Setting and Participants
We analyzed 2016–2019 Medicaid claims data from seven US states.
We defined a heart failure admission as one in which either the admission diagnosis or the first or second clinical (discharge) diagnosis bore an ICD-10 code for heart failure. A readmission was an admission for any condition (not necessarily heart failure) that occurred within 30 days of a heart failure discharge.
Methods
We estimated a mixed-effects logistic model to predict 30-day readmission from patient demographic data, comorbidities, past healthcare utilization, and characteristics of the index hospitalization. We evaluated model fit graphically and measured predictive accuracy by the area under the receiver operating characteristics curve (AUC).
Results
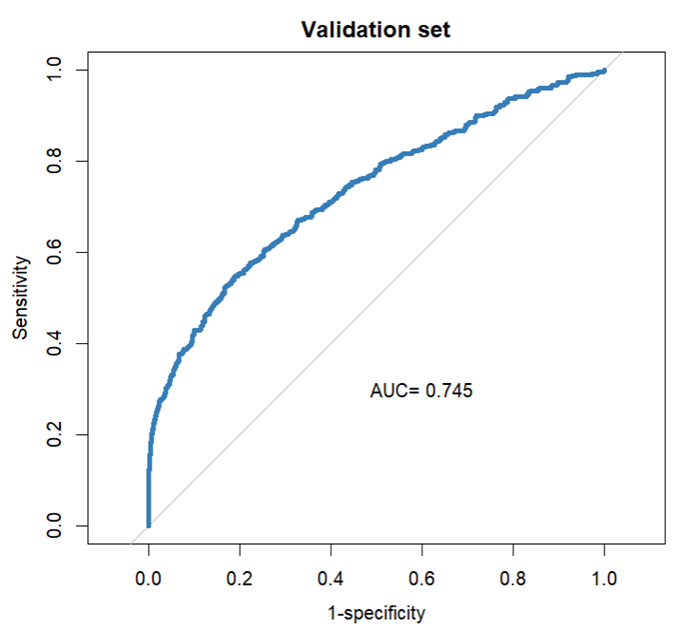
6,859 patients contributed 9,336 heart failure hospitalizations; 2,667 (28.6 percent) were 30-day readmissions. The final model included age, number of admissions and emergency room visits in the preceding year, length of stay, discharge status, index admission type, US state of admission, and past diagnoses. The observed vs. predicted plot showed good fit, and the estimated AUC of 0.745 was robust in sensitivity analyses.
Conclusions and Implications
Our model robustly and with moderate precision identifies Medicaid patients hospitalized for heart failure who are at a high risk of readmission. One can use the model to guide the development of post-discharge management interventions for reducing readmissions and for rigorously adjusting comparisons of 30-day readmission rates between sites/providers or over time.
Keywords: Burden of heart failure; claims database analysis; hospital admissions; Medicaid; prediction model
Introduction
Roughly 2.1 percent of Americans had heart failure between 2015 and 2018, giving rise to an estimated annual cost of $30.7 billion.1 Heart failure is the second-leading cause of hospitalization in the United States and the leading cause of hospitalization among adults over 65.2 Patients with heart failure have elevated rates of all-cause mortality, and they are at higher risk of 30-day readmission when hospitalized for other conditions.3
The medical community has long sought to identify heart failure patients who are at elevated risk for readmission and to craft interventions for improving post-discharge management, with many authors having devised models for predicting 30-day readmission in this population. Although there are now several such models aimed at Medicare patients with heart failure,4 5 6 7 8 9 10 11 to the best of our knowledge only one such model has been derived from Medicaid patients specifically. 12
The Medicaid program, jointly funded by federal and state governments, provides medical insurance to low-income US individuals.13 The single largest source of health insurance in the US, it covers nearly 86 million Americans including children, pregnant women, low-income adults, and individuals with disabilities.14 15 Given the scope of Medicaid and the distinctive characteristics of the covered population,16 there is a need for readmission models that are designed for this set of patients.17 18 We address this gap by using a large Medicaid claims database to develop a novel model for predicting the risk of 30-day readmission among Medicaid patients hospitalized for heart failure.
Methods
Data
We retrieved Medicaid claims through a system operated by Digital Health Cooperative Research Centre (DHCRC), an Australian healthcare research organization, and HMS, Inc. (now part of Gainwell Technologies), a US healthcare analytics company that coordinates Medicaid benefits in several states. We extracted data from the claims, eligibility, and provider databases. The claims database consists of four files comprising institutional, medical, pharmacy, and dental data for each patient encounter. The institutional file includes information on the hospitals and other facilities where the encounters took place; encounter-specific provider data; and patient data such as presenting diagnoses and conditions (represented by International Classification of Disease [ICD] 10 codes). The eligibility database contains patient demographics, eligibility criteria, and dates of eligibility. The provider database includes information on medical service providers.
Study cohort
We had access to Medicaid claims from seven US states served by HMS: fee-for-service claims from Florida; Medicaid Managed Care claims from Georgia, Indiana, Kentucky, and Ohio; and claims of both types from Colorado and Nevada. The claims were dated from January 1, 2016, to June 21, 2019, in Florida; to July 1, 2019, in Ohio; to July 26, 2019, in Nevada; and to August 1, 2019, in the other states.
We used ICD-10 codes to identify heart failure patients from two sources: admission codes in hospitalization claims, and clinical diagnosis codes in physician and hospitalization claims. In the physician and hospitalization claims, we defined a patient as having heart failure if any diagnosis field contained an ICD-10 code starting with I50. Through this approach, our cohort included all patients who had a claim indicating diagnosis of heart failure.
Hospital admissions
A heart failure admission was any claim satisfying all the following criteria:
- It was institutional (not professional, pharmacy, or dental);
- It represented an inpatient hospitalization (excluding long-term care, outpatient, rehabilitation, etc.);
- It was designated as a final “admit thru discharge” claim; and
- Heart failure appeared as either the admission diagnosis or the first or second clinical (discharge) diagnosis.
Index hospitalization
We used index admissions from January 1, 2017, or later, allowing us at least one year of patient history prior to each hospitalization. We then excluded as index admissions any admission whose discharge code indicated in-hospital death or transfer to a short-term general hospital, another type of institution not defined in the Medicaid code list, a Critical Access Hospital, or hospice care. We then identified admissions (for any condition) that occurred within 30 days after discharge from a previous admission; we designated these as readmissions. A readmission for heart failure could serve as the index hospitalization for a subsequent readmission if it also met the criteria for an index admission. Figure S1 presents a schematic of the extraction of the data set.
Potential predictors
Our list of potential predictors of readmission appears in Table 1. We used ICD-10 categories to group past, admission, and main diagnoses into a coarser list of variables. A past diagnosis is an ICD-10 code in a diagnosis field from a prior (to the index) hospitalization or physician visit. An admission diagnosis is an ICD-10 code reported in the admission diagnosis field of the index admission — the proximal reason for the hospitalization. A main diagnosis is an ICD-10 code reported in the main diagnosis field of the index hospitalization — the discharge diagnosis for the hospitalization.19
Outcome
The outcome variable was occurrence of a readmission within 30 days of the discharge from the index hospitalization.
Censoring events
Our database does not include information on mortality except for hospitalized individuals who received a discharge code indicative of death. But because it includes eligibility dates, a subject who died at home could nevertheless be censored for follow-up of a preceding index hospitalization. Also, an index admission could be censored if the number of days of eligibility following an index discharge was less than 30. We did not treat admissions with censored follow-up as index admissions, but we did count them as readmissions when they occurred within 30 days of a prior index admission.
Prediction model
We predicted 30-day readmission using a logistic generalized linear mixed model (GLMM) including patient and provider random effects. This model accounts for potential correlation of outcomes within patients or providers; failure to model this correlation could invalidate confidence intervals and statistical tests.20
Handling of count and continuous predictors
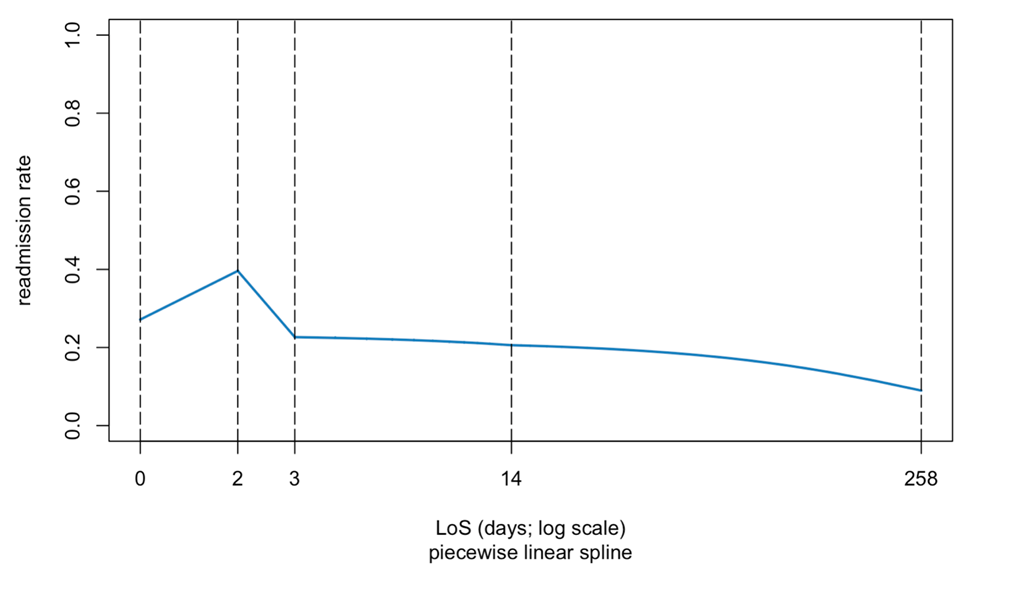
Table 1 includes two count variables (number of hospitalizations and emergency room visits in the 12 months preceding the index hospitalization) that we treated as continuous predictors. We modeled length of stay (LoS) with linear splines to account for the possibility of a complex, non-monotone effect of LoS on readmission risk.21
Model development
We identified the best set of predictors using LASSO variable selection in the R package glmnet.22 This procedure seeks to balance model fit with model complexity, including only variables that contribute substantially to predictive value. With the large number of records in the database, it was impractical to apply the LASSO with the logistic GLMM; therefore, in the model selection step, we used logistic regression without patient and provider random effects. Having identified the best set of predictors, we re-estimated the coefficients of the selected model including the patient and provider random effects. We evaluated the model’s predictive accuracy by computing the area under the receiver operating characteristic curve (AUC). We applied a five-fold cross-validation technique to avoid overfitting bias.23 We assessed significance of predictors in the final GLMM using Wald tests and 95% confidence intervals for regression coefficients. To evaluate calibration, we created a plot of observed versus predicted probability of 30-day readmission.
Missing values
Most variables had few missing values. Among demographic factors, age and sex were complete for all patients, but marital status was available only in Nevada, and race/ethnicity was available only in Florida, Colorado, and Nevada. We therefore excluded marital status and race/ethnicity from our predictive models. We also omitted a small fraction of index admissions whose discharges were recorded with codes “reserved for national assignment” in the data dictionary. Finally, we removed a small fraction (< 0.01%) of index admissions that lacked a national provider identifier.
Sensitivity analysis
We assessed robustness by re-estimating the model under a range of conditions:
- Including and excluding the provider random effects.
- Using a more specific case identification method that defined heart failure patients as those who had either i) ≥2 outpatient diagnoses of heart failure or ii) ≥1 hospitalization for heart failure. We re-estimated the predictions using this smaller cohort.
- Excluding index admissions longer than 28 days.
- Including only index admissions where enrollment was continuous for one year before admission and 30 days after discharge.
- Excluding elective admissions.
We executed all computations in Spark (Apache Software Foundation; Wakefield, MA) and R (The R Foundation; Vienna, Austria).
The authors’ Institutional Review Board reviewed the study proposal and determined that it does not meet the criteria of human-subjects research. The authors had full access to the data; we take responsibility for its integrity and the data analysis.
Results
The final study cohort of 6,859 patients accounted for 9,336 hospitalizations, of which 2,667 (28.6 percent) were 30-day readmissions. The median age was 55 years at the time of the earliest claim, and 45.2 percent of the patients were female (Table 2).
Among diagnosis variables associated with the index admission, the LASSO procedure eliminated the heart failure type and the admission and main diagnosis, retaining several prior diagnosis indicators. Table 3 presents the coefficients in the selected prediction model. A plot of observed versus expected deciles of 30-day readmission probabilities (Figure S2) demonstrates that the predicted and observed readmission rates closely match. Figure 1 presents the ROC curve for the final model, whose AUC is 0.745. Figure S3 presents estimated readmission rate as functions of LoS of the index admission, showing higher readmission rates for very short stays.
Sensitivity analysis
We excluded the provider random effect from the logistic GLMM and re-ran our model including only the patient random effects. This model gave an AUC of 0.733, similar to the AUC obtained from the model that included provider random effects.
We re-estimated the model using the cohort identified by a more specific heart failure case definition that excluded a small fraction (1.7 percent) of patients. This model selected all predictors and past diagnoses in Table 3, giving an AUC of 0.745 — the same as the model using the full data set.
We were concerned that a small fraction (2.0 percent) of index hospitalizations that exceeded 28 days would unduly influence predictions. Re-running the logistic GLMM excluding these observations resulted in an AUC of 0.745, the same as from the model based on the full data set.
We re-ran the model excluding 2,401 subjects (35.0 percent) whose 3,138 hospitalization claims had non-continuous enrollment for a year before or 30 days after admission, yielding an estimated AUC of 0.774. This suggests that having more complete information on previous claims leads to superior prediction.
Patients hospitalized electively were not likely admitted for decompensated heart failure.24 Excluding 886 (9.5 percent) index admissions that were designated as elective, we obtained an AUC of 0.762.
Discussion
We used Medicaid claims data to develop and validate a model predicting 30-day readmissions in patients hospitalized for heart failure. Unlike existing heart failure readmission models, which often use electronic health record fields and include a heterogeneous mix of payers, we built our model with only claims data from a Medicaid population. Our model performed at least as well as others that use more granular clinical and pharmacy claim data. Given the higher readmission rates among Medicaid patients hospitalized for heart failure compared to those insured by other payers, 12 our model may be useful for identifying patients at elevated risk for readmission and targeting post-discharge management interventions to reduce readmissions and contain costs.
Among Medicaid patients with heart failure hospitalized in 7 states between 2016 and 2019, 28.6 percent of admissions resulted in readmission within 30 days of discharge. This is similar to overall 30-day readmission rates observed in studies including mixed insurance coverage but larger than the rate in a previous Medicaid cohort.12 We observed wide variation in readmission rates across the seven states in our analysis (11.9 percent to 33.7 percent; Table 2), a pattern similar to that observed with overall 30-day Medicaid readmissions across states.17 This variation likely reflects heterogeneity in eligibility, coverage, management, and readmission reduction efforts at the state level. Our study is consistent with previous work that has examined readmissions in patients with heart failure and found that age, number of prior admissions and ER visits, length of stay, and post-discharge care environment are independent predictors of readmission. The predictors differ somewhat from those observed in a previous study that included 1,198 Medicaid and 3,350 commercially insured patients. 12
In contrast to some previous studies that have described a positive association between increasing length of stay and readmission risk in patients with heart failure, our analysis using a spline regression model suggests that the relationship between LoS and readmission risk is non-monotone, with an early peak in readmissions at two days and declining thereafter. Others have described a similar non-monotone relationship between LoS and readmission risk in heart failure readmissions.24 Our model selection procedure omitted male sex, which typically predicts a higher readmission rate.
The predictive accuracy of our claims-only 30-day readmission risk model for Medicaid patients with heart failure is moderate and comparable to those noted in recent papers. A 2011 review article25 identified six models for predicting readmission in heart failure — three from retrospective administrative data 6 26 and three from real-time administrative data and retrospective primary data collection.5 27 28 Of those analyses that evaluated predictive accuracy by AUC, none exceeded 0.72.5 Among several readmission models created since 2011,6 29 8 9 10 11 12 only one,9 applying a naïve Bayes classifier to electronic health record data, gave an AUC (0.78) comparable to ours. The only model that specifically uses claims data — taken from Medicaid and commercial insurance — found an AUC of 0.64. 12 By contrast, models for prediction of mortality in heart failure cohorts have generally achieved high accuracy; the model of Amarasingham, for example, gives an AUC of 0.86. 518
Our model has several novel elements: First, we use splines to flexibly model non-monotone trends. Second, we include state as a predictor to account for the heterogeneity of Medicaid coverage, programs, and readmission initiatives. Finally, we include multiple index admissions for each subject and each provider by estimating a GLMM rather than a logistic model that includes only a single observation per patient, as is common in healthcare prediction models.
Although at least one previous heart failure prediction model explicitly included Medicaid claims, 12 ours is the first to focus exclusively on the Medicaid population, which has higher rates of heart failure complications and readmissions than Medicare and commercially insured populations.16 Payer type is an important predictor in readmission models in the US and reflects the underlying patient populations covered. Medicaid payer status is an independent risk factor for readmission,26 as covered patients are poorer, have higher rates of chronic conditions, and possess socioeconomic disadvantages that are difficult to quantify.16 30 We found the post-discharge environment to be a significant predictor of readmission, possibly reflecting the level of social support available.
Our model may be useful in programs to prevent readmission. At the hospital level, one could implement the prediction calculation as a clinical decision support (CDS) tool in the electronic health record system, 31 32 enabling deployment of tailored care-transition services to patients at highest risk.33 Because the prediction equation involves some factors that only become known at discharge — discharge diagnosis and code and length of stay — one might implement a provisional calculation, for example calculating the readmission probability should the patient be discharged to an institution at the current date. Patients whose predicted probabilities of readmission are high would be retained and re-evaluated for discharge at a later time. At the health system level, one could reallocate resources to hospitals that have larger numbers of high-risk patients, or to institutions (such as rehabilitation hospitals) that commonly admit high-risk heart failure patients who are discharged from hospitals.
The discharge code (home or institution) and the length of stay are the only factors in our model on which intervention is possible. But because we have estimated a predictive model rather than a causal model, the odds ratios associated with these factors may not reflect the effects we would observe by intervening on them. A readmission prevention plan based on our model (or any predictive model) should be evaluated in a randomized trial.
To evaluate the potential cost saving from reducing readmissions in heart failure, consider that there are (in rough terms) 1 million heart failure hospitalizations per year, with 10 percent covered by Medicare, at an average cost of $11,000. 34 Our data suggest that about 20 percent of these cases, or 20,000 total, are readmissions. Then a program that would reduce readmissions by only 10 percent would prevent 2,000 readmissions for a savings of $22,000,000 annually in Medicaid alone. This is a conservative figure, as evaluations of AI-supported prevention systems have found that one can reduce the number of readmissions by 14 percent or more. 31 32
A strength of our study is its sole focus on Medicaid patients with heart failure — a large but understudied population that is at high risk for readmission. The pooling of Medicaid claims data from seven states enhances the generalizability of our model and provides a larger sample size than many previous studies of heart failure readmissions.
Our study has several limitations: Although our data set is derived from several states in the South, Midwest, and West, it does not constitute a probability sample of all Medicaid claims, and therefore estimates of readmission rates and the effects of risk factors may not be generalizable to the entire US population. A second potential source of bias is the exclusion of patients who were not continuously enrolled in Medicaid, which could lead to missed index hospitalizations and readmissions. A third is the unavailability of factors that are likely to affect readmission risk such as race, marital status, patient satisfaction, and quality of patient-provider communication; their absence could bias the effects of other factors that appear in the model. Finally, because our claims data are de-identified, we cannot link them to the National Death Index, and therefore we likely failed to capture all deaths.
A recent article from our group estimated a statistical model for 30-day readmission in Medicaid patients diagnosed with diabetes.35 Using similar methods, the final model included age, sex, age-sex interaction, past diagnoses, US state of admission, number of admissions in the preceding year, index admission type, index admission diagnosis, discharge status, LoS, and the LoS-sex interaction. As with our heart failure analysis, the diabetes model fit well, and the estimated AUC of 0.761 was robust in sensitivity analyses and superior to AUCs found in other studies, even those using more granular data sets.
Conclusions and Implications
In this study, we derived and validated a claims-only statistical model to predict 30-day readmissions for hospitalized Medicaid patients with heart failure. Our model shows moderate accuracy similar to other models that are based on more detailed clinical and demographic data. It may be of use to health plans, policy makers, and health systems as they seek to risk-stratify populations and refine, develop, and target interventions to help contain readmission-related costs in Medicaid programs. Future work, including external validation of the risk model within Medicaid programs at the state or payer level, can facilitate the design of readmission-reduction initiatives to reduce morbidity and healthcare costs.
References
1. Virani SS, Alonso A, Aparicio HJ, et al. Heart disease and stroke statistics—2021 update: A report from the American Heart Association. Circulation. 2021;143(8):e254-e743. doi: 10.1161/CIR.0000000000000950.
2. McDermott KW, Roemer M. Most frequent principal diagnoses for inpatient stays in US hospitals, 2018. Healthcare Cost and Utilization Project. 2021. doi: 10.4135/9.
3. Soh JGS, Wong WP, Mukhopadhyay A, Quek SC, Tai BC. Predictors of 30-day unplanned hospital readmission among adult patients with diabetes mellitus: A systematic review with meta-analysis. BMJ Open Diabetes Research & Care. 2020;8(1). doi: 10.1136/bmjdrc-2020-001227.
4. Keenan PS, Normand ST, Lin Z, et al. An administrative claims measure suitable for profiling hospital performance on the basis of 30-day all-cause readmission rates among patients with heart failure. Circulation: Cardiovascular Quality and Outcomes. 2008;1(1):29-37. doi: 10.1161/CIRCOUTCOMES.108.802686.
5. Amarasingham R, Moore BJ, Tabak YP, et al. An automated model to identify heart failure patients at risk for 30-day readmission or death using electronic medical record data. Medical Care. 2010;48(11):981-988. doi: 10.1097/MLR.0b013e3181ef60d9.
6. Hammill BG, Curtis LH, Fonarow GC, et al. Incremental value of clinical data beyond claims data in predicting 30-day outcomes after heart failure hospitalization. Circulation: Cardiovascular Quality and Outcomes. 2011;4(1):60-67. doi: 10.1161/CIRCOUTCOMES.110.954693.
7. Au AG, McAlister FA, Bakal JA, Ezekowitz J, Kaul P, van Walraven C. Predicting the risk of unplanned readmission or death within 30 days of discharge after a heart failure hospitalization. American Heart Journal. 2012;164(3):365-372. doi: 10.1016/j.ahj.2012.06.010.
8. Frizzell JD, Liang L, Schulte PJ, et al. Prediction of 30-day all-cause readmissions in patients hospitalized for heart failure: Comparison of machine learning and other statistical approaches. JAMA Cardiology. 2017;2(2):204-209. doi: 10.1001/jamacardio.2016.3956.
9. Shameer K, Johnson KW, Yahi A, et al. Predictive modeling of hospital readmission rates using electronic medical record-wide machine learning: A case-study using Mount Sinai heart failure cohort. Pacific Symposium on Biocomputing. 2017;22:276-287.
10. Golas SB, Shibahara T, Agboola S, et al. A machine learning model to predict the risk of 30-day readmissions in patients with heart failure: A retrospective analysis of electronic medical records data. BMC Med Inform Decis Mak. 2018;18(1). doi: 10.1186/s12911-018-0620-z.
11. Awan SE, Bennamoun M, Sohel F, Sanfilippo FM, Dwivedi G. Machine learning‐based prediction of heart failure readmission or death: Implications of choosing the right model and the right metrics. ESC Heart Failure. 2019;6(2):428-435. doi: 10.1002/ehf2.12419.
12. Allen LA, Smoyer Tomic KE, Smith DM, Wilson KL, Agodoa I. Rates and predictors of 30-day readmission among commercially insured and Medicaid-enrolled patients hospitalized with systolic heart failure. Circulation: Heart Failure. 2012;5(6):672-679. doi: 10.1161/CIRCHEARTFAILURE.112.967356.
13. Centers for Medicare & Medicaid Services. Medicaid and CHIP beneficiary profile: Characteristics, health status, access, utilization, expenditures, and experience. Center for Medicaid and CHIP Services. 2020.
14. Medicaid.gov. Medicaid eligibility. Medicaid.gov web site. https://www.medicaid.gov/medicaid/eligibility/index.html Accessed 12-23-2021.
15. Medicaid.gov. June 2023 Medicaid & CHIP enrollment data highlights. Medicaid.gov web site. https://www.medicaid.gov/medicaid/program-information/medicaid-and-chip-enrollment-data/report-highlights/index.html. Accessed 10-19-2023.
16. Regenstein M, Andres E. Reducing hospital readmissions among Medicaid patients: A review of the literature. Quality Management in Health Care. 2014;23(4):203-225. doi: 10.1097/QMH.0000000000000043.
17. Trudnak T, Kelley D, Zerzan J, Griffith K, Jiang HJ, Fairbrother GL. Medicaid admissions and readmissions: Understanding the prevalence, payment, and most common diagnoses. Health Affairs. 2014;33(8):1337-1344. doi: 10.1377/hlthaff.2013.0632.
18. Billings J, Dixon J, Mijanovich T, Wennberg D. Case finding for patients at risk of readmission to hospital: Development of algorithm to identify high risk patients. BMJ. 2006;333:327-330. doi: 10.1136/bmj.38870.657917.AE.
19. Center for Medicare and Medicaid Services. CMS guidance: Diagnosis, procedure codes. https://www.medicaid.gov/medicaid/data-and-systems/macbis/tmsis/tmsis-blog/entry/51965 Web site. Updated 2020. Accessed 08-01-2021.
20. Stroup WW. Generalized linear mixed models: Modern concepts, methods, and applications. CRC Press; 2012.
21. Durrleman S, Simon R. Flexible regression models with cubic splines. Statistics in Medicine. 1989;8(5):551-561. doi: 10.1002/sim.4780080504.
22. Hastie T, Qian J, Tay K. An introduction to glmnet. http://glmnet.stanford.edu/articles/glmnet.html Updated 2023. Accessed 07-17-2023.
23. Harrell FE, Lee KL. Regression modeling strategies for improved prognostic prediction. Statistics in Medicine. 1984;3:143-152.
24. Sud M, Yu B, Wijeysundera HC, et al. Associations between short or long length of stay and 30-day readmission and mortality in hospitalized patients with heart failure. JACC. Heart failure. 2017;5(8):578-588. doi: 10.1016/j.jchf.2017.03.012.
25. Kansagara D, Englander H, Salanitro A, et al. Risk prediction models for hospital readmission: A systematic review. JAMA. 2011;306(15):1688-1698. doi: 10.1001/jama.2011.1515.
26. Philbin EF, Disalvo TG. Prediction of hospital readmission for heart failure: Development of a simple risk score based on administrative data. Journal of the American College of Cardiology. 1999;33(6):1560-1566. doi: 10.1016/s0735-1097(99)00059-5.
27. Billings J, Mijanovich T. Improving the management of care for high-cost Medicaid patients. Health Affairs. 2007;26(6):1643-1654. doi: 10.1377/hlthaff.26.6.1643.
28. Krumholz HM, Chen Y, Wang Y, Vaccarino V, Radford MJ, Horwitz RL. Predictors of readmission among elderly survivors of admission with heart failure. American Heart Journal. 2000;139:72-77.
29. Ash AS, Ellis RP, Pope GC, et al. Using diagnoses to describe populations and predict costs. Health Care Financing Review. 2000;21:7-28.
30. Ku L, Ferguson C. Medicaid works: A review of how public insurance protects the health and finances of children and other vulnerable populations. George Washington University Department of Health Policy, and First Focus. 2011.
31. Romero-Brufau S, Wyatt KD, Boyum P, Mickelson M, Moore M, Cognetta-Rieke C. Implementation of artificial intelligence-based clinical decision support to reduce hospital readmissions at a regional hospital. Appl Clin Inform. 2020;11(04):570-577. doi: 10.1055/s-0040-1715827.
32. Wu CX, Suresh E, Phng FWL, et al. Effect of a real-time risk score on 30-day readmission reduction in Singapore. Appl Clin Inform. 2021;12(02):372-382. doi: 10.1055/s-0041-1726422.
33. Kripalani S, Theobald CN, Anctil B, Vasilevskis EE. Reducing hospital readmission rates: Current strategies and future directions. Annual Review of Medicine. 2014;65(1):471-485. doi: 10.1146/annurev-med-022613-090415.
34. Jackson SL, Tong X, King RJ, Loustalot F, Hong Y, Ritchey MD. National burden of heart failure events in the United States, 2006 to 2014. Circulation: Heart Failure. 2018;11(12):e004873. doi: 10.1161/CIRCHEARTFAILURE.117.004873.
35. Yun J, Filardo G, Ahuja V, Bowen ME, Heitjan DF. Predicting hospital readmission in Medicaid patients with diabetes using administrative and claims data. American Journal of Managed Care. 2023;29(8). doi: 10.37765/ajmc.2023.89409.
Table 1. Candidate predictors of readmission
|
Type of variable
|
Variable
|
|
Demographics
|
Age
Sex
US state
|
|
Previous claims
|
Past diagnoses (comorbidity)
Number of admissions in previous 12 months
Number of emergency room visits in previous 12 months
|
|
Index hospitalization
|
Admission type (emergency or non-emergency)
Heart failure type
Length of stay
Discharge code
|
|
Admission diagnoses
|
Admission diagnosis group
Main diagnosis group
|
Table 2. Summary of Medicaid data on patients with heart failure from seven US states
|
State
|
CO
|
FL
|
GA
|
IN
|
KY
|
NV
|
OH
|
Total
|
|
Patients
|
1,921
|
461
|
148
|
149
|
788
|
1,925
|
1,467
|
6,859
|
|
Claims
|
2,707
|
493
|
197
|
168
|
1,101
|
2,777
|
1,893
|
9,336
|
|
Agea
|
56 (47–62)
|
53 (43–60)
|
41 (35–48)
|
53 (42–59)
|
56 (49–63)
|
55 (47–60)
|
56 (49–61)
|
55 (47–61)
|
|
Female (%)
|
41.6
|
31.7
|
87.8
|
42.3
|
53.3
|
38.8
|
54.1
|
45.2
|
|
Readmit (%)
|
32.4
|
18.5
|
17.8
|
11.9
|
27.2
|
33.7
|
21.6
|
28.6
|
|
LoSb
|
5.6
|
6.8
|
5.0
|
6.1
|
5.8
|
6.2
|
6.0
|
6.0
|
|
Previous
admissionsc
|
7.5
|
1.4
|
1.5
|
0.8
|
2.5
|
3.3
|
3.1
|
4.2
|
|
Previous ER visitsd
|
8.1
|
2.7
|
4.7
|
1.8
|
4.5
|
5.3
|
6.7
|
6.1
|
|
Discharged to an institution (%)
|
7.4
|
19.7
|
0.5
|
8.9
|
10.9
|
11.2
|
9.7
|
9.9
|
|
Emergent or urgent type admissions
|
92.0
|
95.3
|
93.9
|
86.9
|
86.5
|
88.4
|
90.3
|
90.1
|
aMedian (1st quartile – 3rd quartile)
bAverage length of stay.
cAverage number of admissions in 12 months preceding the index claim.
dAverage number of emergency room visits in 12 months preceding the index claim.
Table 3. Final prediction model
|
Type of variable
|
Variable
|
Odds ratio (95% CI)
|
|
Demographic
|
Age
|
0.98 (0.98,0.99)
|
|
Previous claims
|
# admits last 12 months
|
1.15 (1.13,1.17)
|
|
# emergency room visits last 12 months
|
1.00 (0.99,1.01)
|
|
Length of stay
|
LoS spline
|
See Figure S3
|
|
Discharge code
(reference is discharged home)
|
Discharged to an institution
|
1.68 (1.39,2.02)
|
|
Admission type (reference is emergency)
|
Non-emergency
|
0.78 (0.63,0.95)
|
|
US state of claim (reference is Colorado)
|
Florida
|
0.80 (0.58,1.10)
|
|
Georgia
|
0.89 (0.56,1.40)
|
|
Indiana
|
0.50 (0.27,0.92)
|
|
Kentucky
|
1.27 (1.02,1.58)
|
|
Nevada
|
1.41 (1.19,1.68)
|
|
Ohio
|
0.80 (0.66,0.97)
|
|
Past diagnosis
(reference is absence of the condition)
|
Blood disorders
Cardiac arrhythmia
Chronic lower respiratory diseases
Health services for specific procedures
Hemolytic anemia
Ischemic heart disease
Obesity
Renal failure
Sepsis
|
1.21 (1.03,1.42)
1.05 (0.92,1.20)
1.13 (0.99,1.28)
1.07 (0.94,1.22)
1.18 (1.03,1.34)
1.06 (0.93,1.21)
0.89 (0.79,1.01)
1.30 (1.13,1.49)
1.09 (0.96,1.25)
|
Figure 1. The ROC curve for the final prediction model
SUPPLEMENTAL MATERIAL
Predicting readmission in Medicaid patients hospitalized for heart failure using administrative and claims data
Supplemental Figure Legends
Supplemental Figure 1. Schematic of extraction of the data set.
Supplemental Figure 2. Observed versus expected plot showing deciles of 30-day readmission predicted probability.
Supplemental Figure 3. Linear splines for length of stay in the prediction model.
Figure S1. Schematic of extraction of the data set
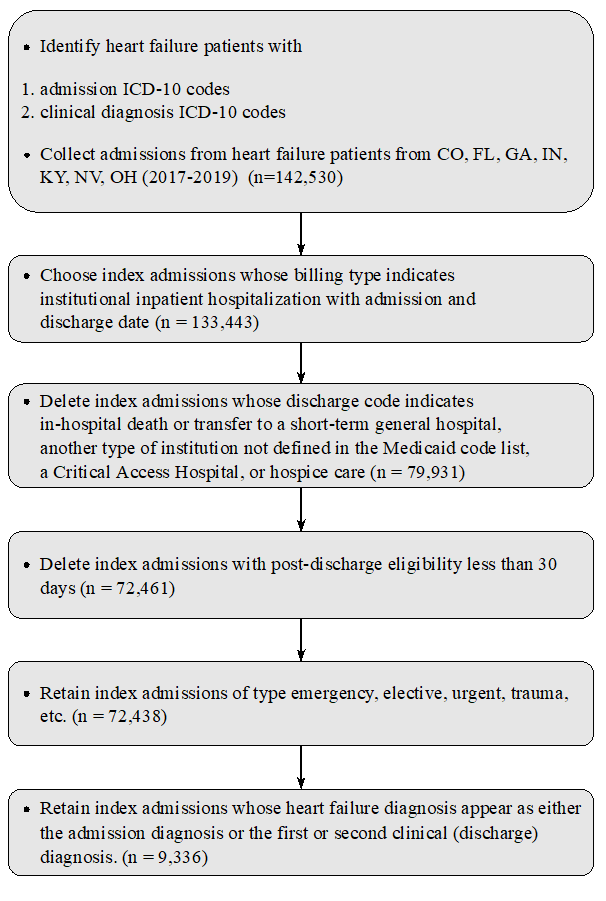
Figure S2. Observed versus expected plot showing deciles of 30-day readmission predicted probability. The diagonal line indicates where the points would lie in a perfectly calibrated model.
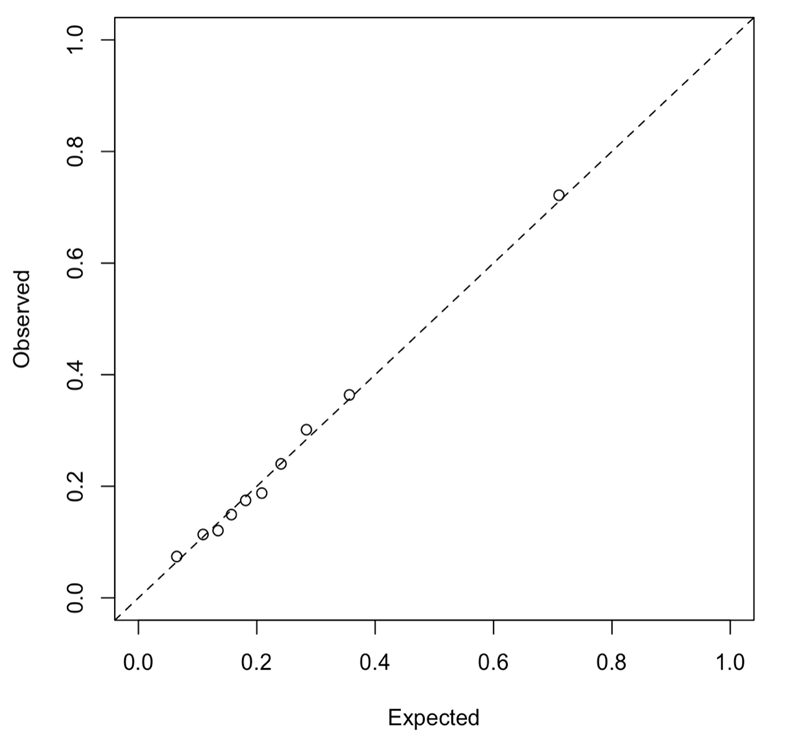
Figure S3. Linear splines for length of stay in the prediction model
Author Biographies
Jaehyeon Yun (jaehyeon.yun@gainwelltechnologies.com) is a data scientist at Gainwell Technologies.
Vishal Ahuja (vahuja@smu.edu) is associate professor of information technology and operations management at the Southern Methodist University Cox School of Business and Adjunct Faculty at the University of Texas Southwestern Medical Center.
Daniel F. Heitjan (dheitjan@smu.edu) is professor and chair of statistics and data science at Southern Methodist University and Professor of Public Health at the University of Texas Southwestern Medical Center.